Week 6: Unsupervised Learning:
Topic Models
Let’s quickly review your future assignments:
Problem Set 1
Problem Set 2
Project Proposal
We started from pre-processing text as data, representing text as numbers, describing features of the tex, and learned how to measure concepts in text:
Data: humans, documents, votes, etc. are not pre-labelled in terms of some underlying concept.
Goal: take the observations and find hidden structure and meaning in them
Main models we will learn:
Clustering Models
Topic Models
Unsupervised learning requires several ad-hoc decisions and these decisions matter for quality of your results
Domain knowledge (and honestly a bit of randomness) guides a lot of these decisions
In contrast to supervised approaches, we won’t know ‘how correct’ the output
Use statistical measures of fit/unfit of different modeling decisions
No easy measure of accuracy, recall and precision.
Purpose: look for ‘groups’ in data explicitly.
Clusters: group of data points that are all nearby to each other and far away from other clusters.
Research Questions? How can we categorize these news articles or policy bills? How can we group these legislators based on their speeches?
K-Means clustering: partition the docs into a set of K categories where docs with similar rates of word usage are assigned to the same cluster and dissimilar docs are assigned to different categories
Pre-specify cluster numbers
Algorithm puts observations into clusters which minimize the within-cluster sum of squares (i.e., sum of squared Euclidean distances between each data point and its assigned cluster centroid)
Objective function to minimize
Initialize Clusters centroids randomly (\(\mu_k\))
Assign Documents to nearest centroid clusters using euclidean distance.
Calculate loss function between points and their clusters
\[ J = \sum_{i=1}^{n} \sum_{k=1}^{K} r_{ik} \, \| x_i - \mu_k \|^2 \]
\[ \mu_k = \frac{\sum_{i=1}^{n} r_{ik} \, x_i}{\sum_{i=1}^{n} r_{ik}} \]
| Algorithmic Models | Probabilistic Models | |
|---|---|---|
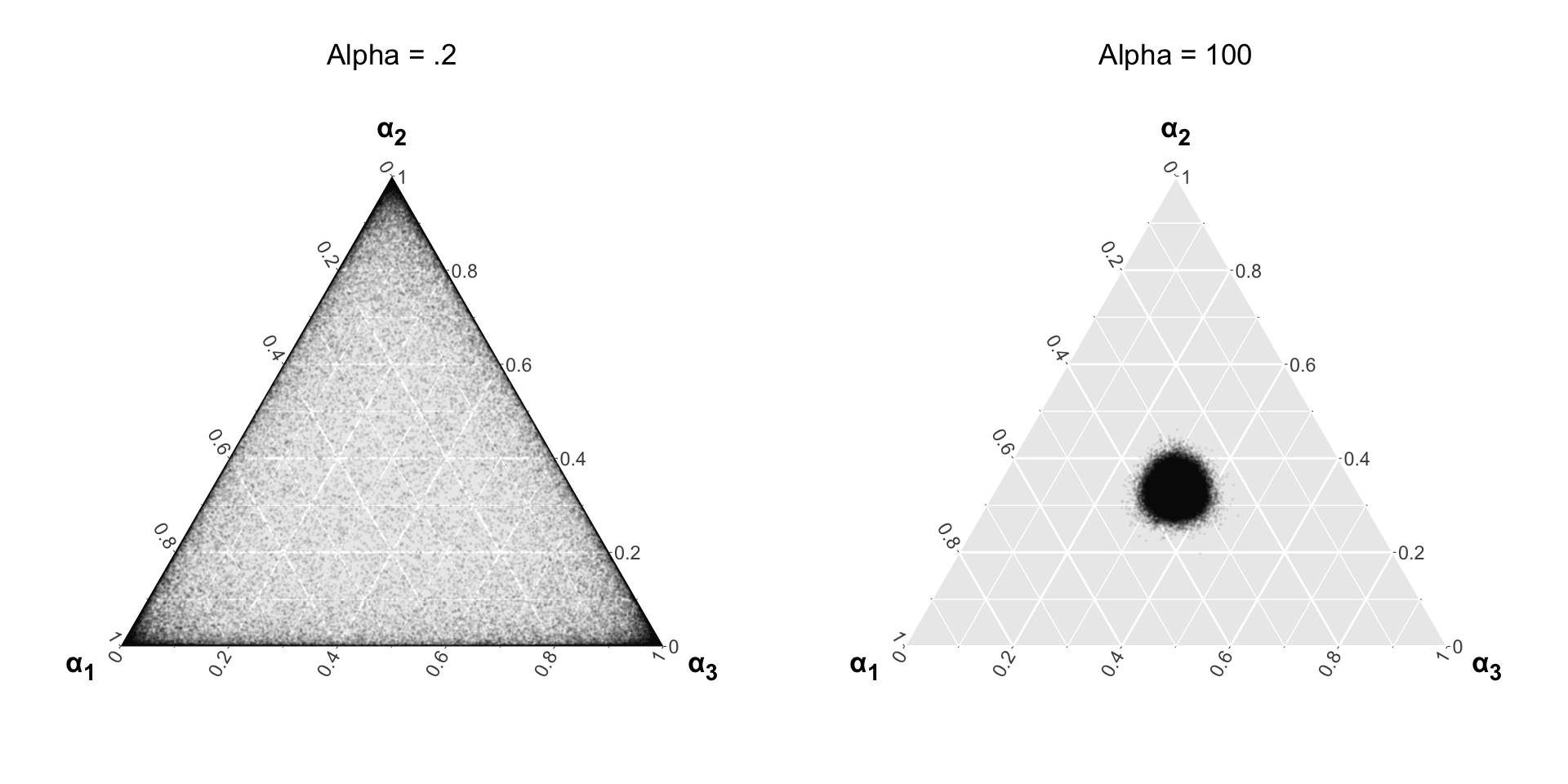
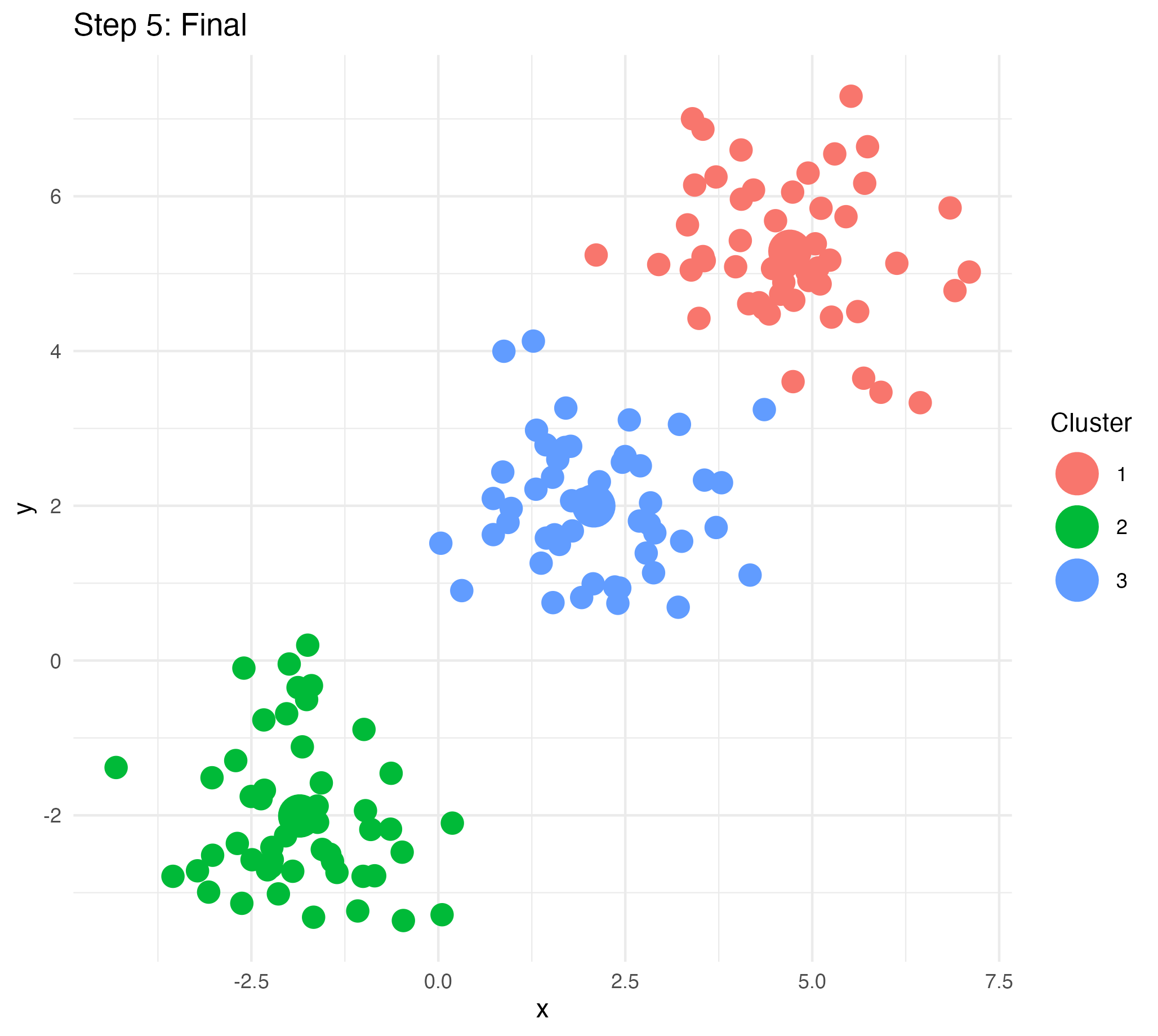
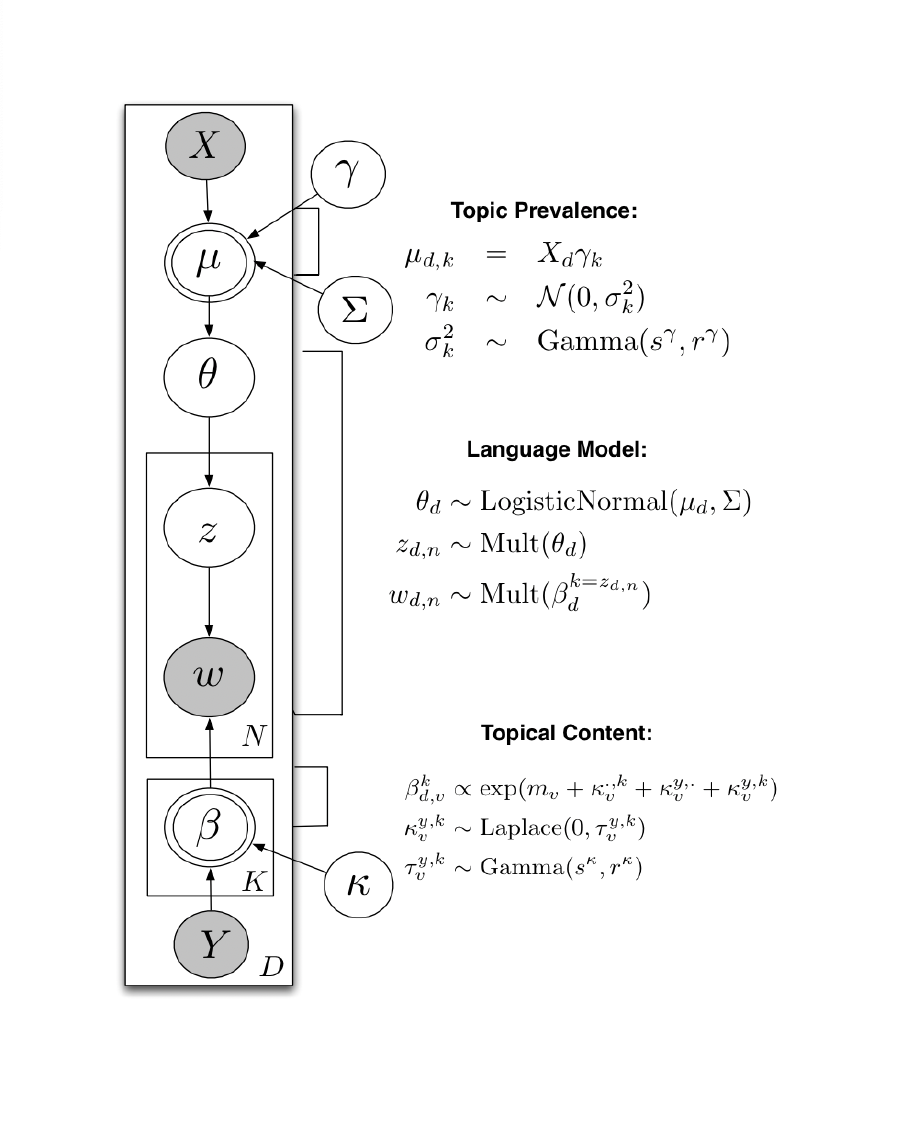
| Idea | learning as an optimization problem | learning as inference based on mathematical model aboout the world |
| Output | Deterministic representations (e.g., clusters, embeddings) | Distributions + uncertainty over latent structures |
| Goal | minimize a cost function | Estimate the likelihood of observed data given certain parameters |
Clustering:
Topic Models:
every document has a probability distribution of topic.
every topic has a probability distribution of words.
use likelihood estimation to find the parameters of these distributions
Problem: Once we start with docs, we do not know what topics exist, what words belong to which topics, what topic proportions each document has
Probabilistic Model: Make assumptions about how language work, and how topics emerge:
Documents: formed from probability distribution of topics
Topics: formed from probability distribution over words
Step 1: For each document:
Step 2: For each topic
Step 3: Then, for every word in the document
For each document (and then topic) ~ Randomly choose a distribution from many multinomal distributions
For every word:
Randomly choose a topic from the distribution over topics from step 1.
Randomly choose a word from the distribution over the vocabulary that the topic implies.
To estimate the model, we need to assume some known mathematical distributions for this data generating process:
For every topic: Each topic k has a word distribution \(\beta_k\) , drawn from a Dirichlet prior:
For every document: Each document d has a topic distribution \(\theta_d\) , drawn from a Dirichlet prior
For every word:
where:
The Dirichlet distribution is a conjugate prior for the multinomial distribution.
It is parameterized by a vector of positive real numbers (\(alpha\))
Larger values of \(\alpha\) (assuming we are in symmetric case) mean we think (a priori) that documents are generally an even mix of the topics.
If \(\alpha\) is small (less than 1) we think a given document is generally from one or a few topics.
Inference: Use the observed data, the words, to make an inference about the latent parameters: the \(\beta\)s, and the \(\theta\)s.
We start with the joint distribution implied by our language model (Blei, 2012):
\[ p(\beta_{1:K}, \theta_{1:D}, z_{1:D}, w_{1:D})= \prod_{K}^{i=1}p(\beta_i)\prod_{D}^{d=1}p(\theta_d)(\prod_{N}^{n=1}p(z_{d,n}|\theta_d)p(w_{d,n}|\beta_{1:K},z_{d,n}) \]
To get to the conditional:
\[ p(\beta_{1:K}, \theta_{1:D}, z_{1:D}|w_{1:D})=\frac{p(\beta_{1:K}, \theta_{1:D}, z_{1:D}, w_{1:D})}{p(w_{1:D})} \]
The denominator is hard complicate to be estimate (requires integration for every word for every topic):
Choosing K is “one of the most difficult questions in unsupervised learning” (Grimmer and Stewart, 2013, p.19)
Common approach: decide based on cross-validated statistical measures model fit or other measures of topic quality.
Working with topic models require a lot of back-and-forth and humans in the loop.
How to measure the quality of the topics?
Crowdsourcing for:
Data: tweets sent by US legislators, samples of the public, and media outlets.
LDA with K = 100 topics
Topic predictions are used to understand agenda-setting dynamics (who leads? who follows?)
Conclusion: Legislators are more likely to follow, than to lead, discussion of public issues,
Take 5-min to read the methods sections of these papers
List to me some of the decisions the authors need to make to get the topic models to work.
Do you think these make sense? What would you do different?
Structural topic model: allow (1) topic prevalence, (2) topic content to vary as a function of document-level covariates (e.g., how do topics vary over time or documents produced in 1990 talk about something differently than documents produced in 2020?); implemented in stm in R (Roberts, Stewart, Tingley, Benoit)
Correlated topic model: way to explore between-topic relationships (Blei and Lafferty, 2017); implemented in topicmodels in R; possibly somewhere in Python as well!
Keyword-assisted topic model: seed topic model with keywords to try to increase the face validity of topics to what you’re trying to measure; implemented in keyATM in R (Eshima, Imai, Sasaki, 2019)
BertTopic: BERTopic is a topic modeling technique that leverages transformers and TF-IDF to create dense clusters of words.
Prevalence: Prior on the mixture over topics is now document-specific, and can be a function of covariates.
Content: distribution over words is now document-specific and can be a function of covariates.
Text-as-Data
